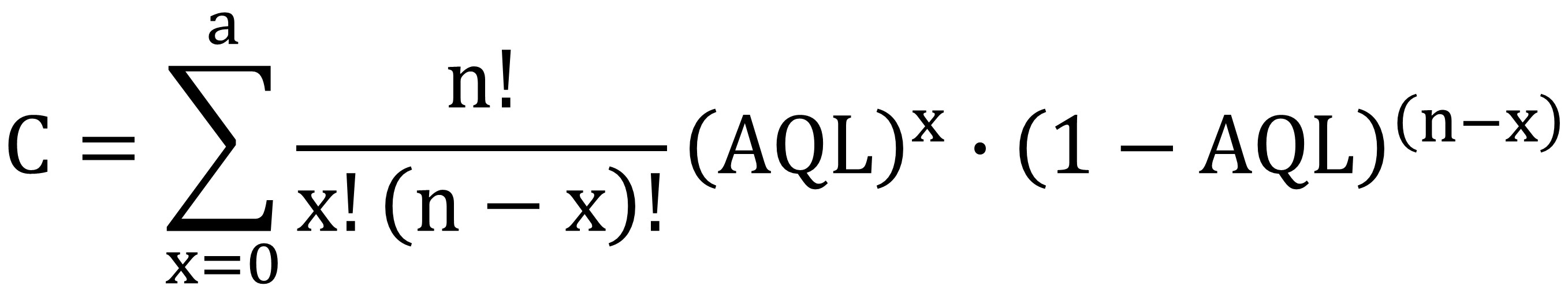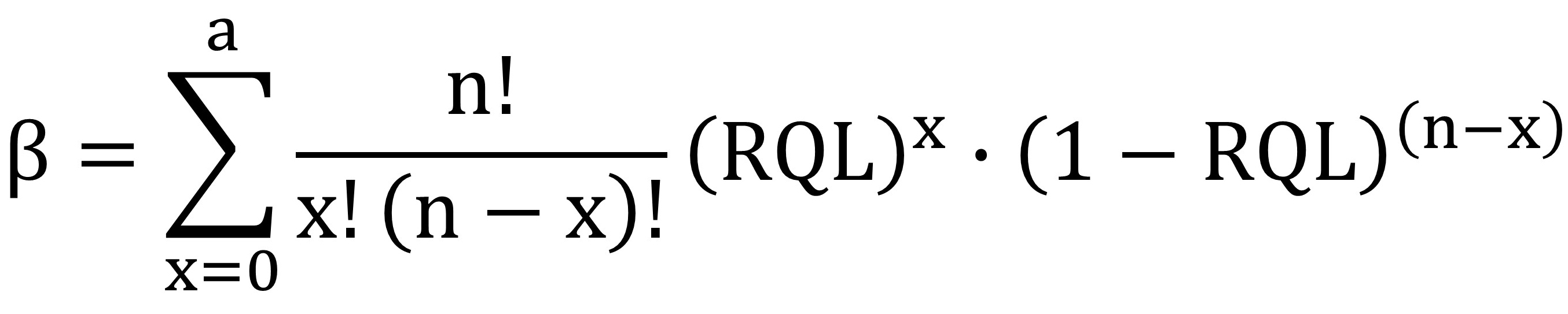Engineered Datalytics, LLC - Online Binomial Data Exploration and Analysis Tool

Comprehensive Binomial Data Sampling Plan Development Tool

Parameter Input

Minimum number of independent, random, and representative samples to be included in the test/inspection.	Alpha = Probability of making a Type I Error or the probability of failing to accept good parts/lots. Known as Manufacture's Risk [Alpha=1-C].
Maximum permissible test sample failures to be oberved before test is considered a failure.	Beta = Probability of Making a Type II Error or the probability of failing to reject non-conforming parts/lots. Known as Customer's Risk [Beta=1-Power].

Design Verification and Process Validation -- One-Shot Reliability Demonstration (Bayes Success Run Theorem)
Design verification involves the generation objective evidence to support the conclusion that the design is capable of meeting the requirements of its engineering input acceptance criteria.
{21 CFR 820.30 (f), 21 CFR 820.250 (a) and (b) | ISO 13485 Sections 7.3.5, 8.1, 8.2.4.1, and 8.4 | ISO 9001-2013 Sections 7.3, 8.1, and 8.4}
Process validation involves the generation objective evidence to support the conclusion that the process is capable of repeatedly producing product that meets the requirements of the design specifications. Let it be assumed that in order to be deemed capable, a process must demonstrate a percent defective is accepted by company policy. {21 CFR 820.75, 21 CFR 820.250 (a) and (b) | ISO 13485 Sections 7.5.2, 8.1, 8.2.4.1, and 8.4 | ISO 9001-2013 Sections 7.5.2, 8.1, and 8.4}

When No. of Defects Equals Zero
Estimated Reliability:

Statistical Conclusion Statement (Design):
Statistical Conclusion Statement (Process) (compare this to the your company's acceptance threshold for allowable PPM defective):

When No. of Defects Does Not Equal Zero


Statistical Conclusion Statement (Design):
Statistical Conclusion Statement (Process): (compare this to the your company's acceptance threshold for allowable PPM defective):

On-Going Manufacturing Quality Control -- AQL | RQL Based Lot Acceptance Sampling

Lot acceptance sampling involves the generation of objective evidence to support the conclusion that the material/components/products being inspected meets design specifications with a centain level of statistical confidence (1-alpha) and statistical power (1-beta). The application of AQL | RQL based sampling plans can be used to determine acceptance/rejection at in-coming inspection, in-process inspection, and out-going inspection. {21 CFR 820.80 (a) |ISO 13485 Sections 7.5.1.1, 8.1, 8.2.4.1, and 8.4| ISO 9001-2013 Sections 7.5.1, 8.1, and 8.4}

Statistical Conclusion Statement:

AQL (Acceptable Quality Limit) The lot percent defective at which there is a "1-alpha" percent chance of accepting the lot and an "alpha" percent chance of rejecting the lot.		IQL (Indifference Quality Limit) The lot percent defective at which there is a 50 percent chance of accepting and/or rejecting the lot.		RQL (Rejectable Quality Limit) The lot percent defective at which there is a "1-beta" percent chance of rejecting the lot and a "beta" percent chance of accepting the lot.

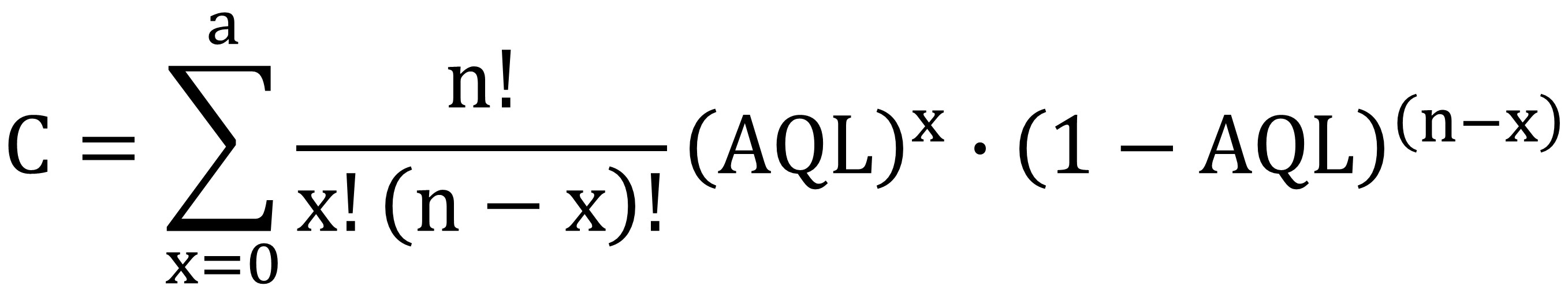
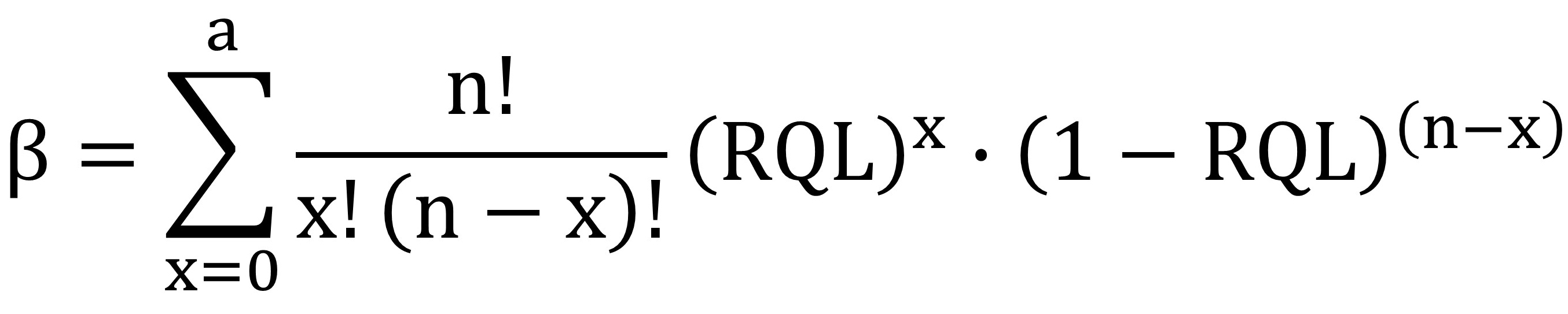
Engineered DataLytics Software Validation File No. 000001 Available for Purchase

Legal Disclaimer "This Engineered DataLytics interactive tool provides easy statistcal exploration and in no manner provides engineering conclusions. It is up to the engineers using this tool to understand the statistical results and apply them appropreiatly as they make at their own engineering decisions."

Online Tool Version v2017-11-26-A. Purchased version includes report generation functionality, software validation file, and is installable on your company's intranet.

Return Home

Consider purchasing the full version of this tool to print reports